Atcoder 泛做

9.2

AGC 047

A - Integer Product

先把每个数乘上 $10^9$，如果两个数的积是整数满足末尾至少有 $18$ 个 $0$ 就行了，即质因子 $2$ 的次数和 $5$ 的次数都要大于等于 $18$，暴力枚举两个数的 $2$ 和 $5$ 的幂次然后算就行了。

B - First Second

可以发现 $S$ 能转换到的字符串是 $S$ 的一个后缀再在前面加一个 $S$ 前面的字母，对所有串建 Trie，然后枚举每串能转换到的串就行了。

C - Product Modulo

求出 $200003$ 的原根 $g$，每个 $a_i$ 用 $g$ 的幂次表示，则 $a_i\times a_j$ 可以转化为对应 $g$ 的幂次的加法，一遍 FFT 就行了。

D - Twin Binary Trees

枚举上面的树选的两个叶子的 LCA 和其中一个叶子，考虑计算 LCA 另一子树对当前枚举的叶子的贡献，枚举下面的树选的两个叶子的 LCA，算下上面的树一个子树的叶子连到下面的树的一个子树的贡献就行。

具体可以先把要算的另一个子树的叶子对应到下面的树的叶子标记一遍其到根的路径。

E - Product Simulation

先考虑两个 $01$ 的乘法怎么搞。

设这两个数是 $x,y$，可以用 $[ [ x+[ x<y ] ]<x+y ]$ 计算。

考虑可以用快速乘的方法做，先预处理出 $2^k$ 和 $2^k \times A$。

问题在于计算 $A\times B \ (B\in \{0,1\})$。

可以爆出 $A$ 的每一个二进制位上的值然后用两个 $01$ 之间的乘法求出这个位真正的值，最后再还原。

爆出 $A$ 的每个二进制位上的值的问题在于计算 $2^k \times B \ (B \in \{0,1\})$。

这个等价于 $B$ 左移 $k$ 位。

操作次数是 $O(\log^3)$ 的。

F - Rooks

先按 $x$ 坐标排序，这样每个点能干掉的点是一个区间。

考虑一个 $O(n^2)$ 的做法。

设 $f_{i,j,0/1}$ 表示 $[i,j]$ 内都被干掉了，现在在 $i$ 或者 $j$ ，接下来干掉能干掉的要跑多远。

转移往左右延伸就行。

把关于 $x$ 坐标和 $y$ 坐标都相邻的点缩起来再记忆化跑这个 dp 就能做到 $O(n\log n)$ 或者实现精细能做到 $O(n)$。

证明不难，读者可尝试自行证明或者点击下面链接。

需要科学上网

9.3

AGC 046

A - Takahashikun, The Strider

显然答案是 $\frac{360}{\gcd(360,X)}$。

B - Extension

令 $dp_{i,j}$ 表示扩充成 $i\times j$ 有多少种方案。

转移考虑减去重复的部分就行了。

$dp_{i,j}=dp_{i-1,j}\times {j}+dp_{i,j-1}\times i - dp_{i-1,j-1}\times (i-1) \times (j-1)$

C - Shift

移动 1 相当于用 0 分割 1，考虑根据这个 dp。

令 $dp_{i,j,k}$ 表示前 $i$ 个 0 前还需要移动 $j$ 个 1 过去，前面用了 $k$ 次操作。

转移枚举当前的 0 前面有几个 1 就行了，操作数在移动 1 到前面的时候再算上就行了。

直接 dp 是 $O(n^4)$，已经能过了，可以加上前缀和优化到 $O(n^3)$。

D - Secret Passage

vp 的时候写了个 $O(n^5)$，然后过了...

考虑最终能搞出来的串就是一个后缀再插入若干个从前面搬来的 0 和 1。

可以先 dp 一遍，求出对于每个后缀插 $i$ 个 0 和 $j$ 个 1 是否可行。

对于一个后缀 $i$ 可以插 $j$ 个 0 和 $k$ 个 1，如果存在一个后缀 $i'(i'>i)$ 可以插若干个 01 变成后缀 $i$ 再可以插 $j$ 个 0 和 $k$ 个 1，那么显然后缀 $i$ 可以插 $j$ 个 0 和 $k$ 个 1 没贡献。

所以只要对所有有贡献的地方算贡献就行了。

再考虑 dp，令 $f_{i,j,k}$ 表示后缀 $i$ 插 $j$ 个 0 和 $k$ 个 1 的方案。

转移就考虑能用串的字符就用串的字符，不用自己可以随便插的字符。

最后算贡献的时候需要单独考虑一下最后一段。

E - Permutation Cover

先考虑无解的情况，不难发现当 $2\times \min(a_i)+1 \le \max(a_i)$ 的时候无解。

考虑贪心的构造答案，每次加入一个新的排列（由末尾的几个加上新加入的几个组成）。

设 $b_i$ 表示这轮加入后 $i$ 还要加几个。

如果 $2 \times \min(b_i) \ge \max(b_i)$，那肯定有解；另外因为前面还有一段，所以 $2 \times \min(b_i) +1 = \max(b_i)$ 也有可能有解，但需要满足所有 $b_j=\min(b_i)$ 的 $j$ 在所有满足 $b_k=\max(b_i)$ 的后面。

每次枚举加入的数的个数，贪心构造方案，在所有合法方案中找一个字典序最小的就行。

复杂度 $O(K^2 \sum{a_i})$。

F - Forbidden Tournament

合法的图一定是一堆大小为 $1$ 的强连通分量后面跟着一个大小任意的强连通分量。

枚举前面强连通分量的个数 $i$，问题转化为求一个大小为 $n-i$ 的强连通分量，入度最多为 $k-i$。

设 $1$ 号节点出边的点的集合为 $T$，入边集合为 $S$。

有以下几个结论：

$S$ 是 DAG。
$T$ 是 DAG。
先设 $S$ 中的点按拓扑序是 $s_1,s_2,...,s_n$，$T$ 中的点按拓扑序是 $t1,t2,...,t_m$，如果存在边 $(t_j,s_i)$ 则一定还会存在边 $(t_{j+1},s_i)$ 和 $(t_{j},s_{i-1})$，如果把一个矩阵的 $(i,j)$ 表示是否存在边 $(t_j,s_i)$，则相当于是如果存在 $(i,j)=1$ 则 $(i-1,j)=1$，$(i,j+1)=1$。

证明可以看官方题解。

考虑枚举 $S$ 的大小，$S$ 到 $T$ 之间的连边的方案可以 $O(n^2)$ dp 对应的矩阵。

复杂度 $O(n^4)$。

dp 矩阵的部分还可以用容斥优化。

9.4

Tokio Marine & Nichido Fire Insurance Programming Contest 2020

A-E 大家应该都会，所以就只记 F。

F - Triangles

考虑皮克定理，问题可以转化为求:

\[ \sum_{y=1}^{W-1} \sum_{1\le x \le z \le H-1} [y\times z+x\times (W-y)-\gcd(x,y)-\gcd(W-y,z)-\gcd(W,z-x) \le 2 \times k-2]\]

考虑枚举 $y,z$，可以毛估估出一个 $x$ 的范围，在这个范围里暴力就行，具体来说大概就是把几个 $\gcd$ 的值都看成最坏情况二分出 $L,R$ 使得当 $x\le L$ 肯定是合法的，$x R $ 的时候肯定是不合法。

不会算复杂度，但是过了。

NOMURA Programming Competition 2020

A-E 大家应该都会，所以就只记 F。

F - Sorting Game

考虑一个序列是合法的需要满足对于每一个逆序对 $(a_i,a_j)$，$a_i$ 和 $a_j$ 二进制上只有一位不一样，且 $a_i$ 不一样的位上的值为 $1$，$a_j$ 为 $0$。

考虑直接 dp，令 $f_{n,m}$ 表示长度为 $m$ 值域为 $[0,2^n)$ 合法的序列数。

转移考虑 $m$ 个数最高位的情况，有两种情况。

最高位上是 000111，这种情况不存在两个地方先 1 后 0，可以直接从 $f_{n-1,m}$ 转移，中间分隔的地方有 $m+1$ 种方案。
最高位上是 0001XXX0111，X 表示是任意值，这种情况下需要保证中间 1XXX0 在低位必须全部相同，相当于把这一部分缩成了一个数，这部分需要枚举最后缩完之后有几个数，设有 $i$ 个数，则有 $i$ 种方案放置中间的 1XXX0，中间的 $X$ 可以随便填，方案是 $2^{m-i-1}$，所以对应方案数是 $\sum_{i=1}^{m-1} i \times 2^{m-i-1} \times f_{n-1,i}$。

第二部分可以用前缀和优化，时间复杂度是 $O(nm)$ 的。

9.7

AGC 045

A - Xor Battle

考虑从后往前做，一个一个数插入线性基，如果 1 号玩家的数插进去了，答案就是 1，不然就是 0。

正确性显然。

B - 01 Unbalanced

vp 的时候写了个乱搞，结果过了...

以下用 $cnt0/cnt1$ 表示一个区间的 0/1 个数。

假装 $\max(cnt0-cnt1)\le x$，目标就是最小化 $\max(cnt1-cnt0)$。

考虑从前往后一个一个问号填，能填 0 就填 0，具体来说就是如果当前位置填 0 剩下的位置全填 1，$\max(cnt0-cnt1)$ 都肯定大于 $x$ 了，就填 1。

显然随着 $x$ 增大，$\max(cnt1-cnt0)$ 单调不增。

考虑二分 $x$，使得两者的值尽可能接近。

然而这样 WA 了一个点，每次再从后往前填在做一遍就行了。

C - Range Set

显然 $A,B$ 可以 swap，所以下面考虑 $A \le B$ 的情况。

不能考虑咋操作去得到序列，而要考虑一个序列能不能通过操作得到。

首先一个最终的序列如果存在长度大于等于 $B$ 的 1 的连续段，显然是可以操作得到的，先把除了这个连续段以外的 1 填完，最后填这段就行了。

可以发现所有长度大于等于 $A$ 的 0 连续段可以全部改成 1，因为这些连续段可以通过最后填 0 得到。

所以一个序列如果不合法就是满足把所有长度大于等于 $A$ 的 0 连续段变成 1，不存在长度大于等于 $B$ 的 1 连续段。

剩下的简单做两遍 dp 就行。

D - Lamps and Buttons

策略是每次找最小的没确定的点，找到环就先把所有环点亮。

如果 GG 的话就是搞到自环或者有环全在后 $N-A$ 个点。

显然一个合法方案最多只能有一个自环。

枚举自环的位置，问题转化为求有 $x+z+y$ 个点，$x$ 个点不能出现自环，$z$ 个点随便，$y$ 个点在的环至少要有一个前 $x$ 个点的方案。

容斥掉自环的条件，问题转化为求有 $x+z+y$ 个点，$x+z$ 个点随便，$y$ 个点在的环至少要有一个前 $x$ 个点。

考虑先插 $x$ 个数，在插 $y$ 个数，最后插 $z$ 个数，可以得到方案是 $\frac{x}{x+y}(x+y+z)!$。

E - Fragile Balls

可以把一个球从 $A_i$ 运到 $B_i$，看做是 $A_i$ 向 $B_i$ 连一条边。

先考虑 $C_i=1$ 的情况，可以发现答案不是 -1，就是 $\sum [A_i\ne B_i]$。

因为每个点都有入度，手玩一下可以发现如果一个弱连通块不是一个大小超过 $1$ 的环，就肯定是合法的。

这提示我们可以把所有弱连通块分成三类。

自环，且只有一条边。
大小大于 $1$ 的环。
除了上面两种。

答案显然至少是 $\sum [A_i\ne B_i]$ 加上大小大于 $1$ 的环的个数。

手玩一下可以发现有 $4$ 种操作种类先扔过去处理大小大于 $1$ 的环，最后再扔回 $B_i$。

第三种连通块里的球，且满足 $A_i\ne B_i$，可以处理 $C_i-1$ 个环，并且不需要额外的代价。
第三种连通块里的球，且满足 $A_i=B_i$，可以处理 $C_i-1$ 个环，但需要一次额外的操作。
第一种连通块里的球，需要先扔进来前两种操作中的一种，然后再去操作，可以处理 $C_i-1$ 个环，因为本身原先是合法的，又需要吞掉前两种操作的中的一次操作，所以实际能处理的应该是 $C_i-2$ 个环，并且需要两次额外的操作。
第二种连通块里的球，也需要先扔进来前两种操作中的一种，可以处理 $C_i-1$ 个环，因为本身原先就是不合法的，所以实际能处理的就是 $C_i-1$ 个环，并且不需要额外的操作。

接下来随便贪心，two pointers 搞搞就行了。

F - Division into Multiples

可以转化为 $A,B,C$ 两两互质的情况，具体怎么搞可以看这里。

我们称一个二元组 $(p,q)$ 是好的，需要满足 $p\times A+q\times B \equiv 0 \ (\bmod \ C)$，且找不到一对满足上一个条件的 $(p',q')$ 使得两个数都比 $(p,q)$ 小。

设 $D=\dfrac AB \mod C$，我们就是相当于要找所有的 $i$ 满足对于任意 $j \ (j<i)$，都有 $Di \mod C < Dj \mod C$。

具体找的过程可以看这里，大概是一个类似欧几里得算法的过程。

可以观察到所有好的二元组是 $O(\log)$ 个等差数列的形式，并且满足 $x_i-x_{i-1}\le x_{i+1}-x_i,y_{i-1}-y_{i}\ge y_i-y_{i+1}$，由于这个性质，选的二元组的种类肯定是同一个或者相邻的，因为如果一对 $(i,j)$ （$i,j$ 表示选的二元组的下标）满足 $j-i\ge 2$，显然选择 $(i+1,j-1)$ 更优秀。

于是只要考虑计算每一个等差数列就行了。

对于一个等差数列，设这条线段的左上角是 $(xl,yl)$ 右下角是 $(xr,yr)$，二分答案，考虑怎么 check，显然每个选的二元组 $(p,q)$ 满足 $p\ge xl,q\ge yr$，可以先减去。这条线段上的一个二元组 $(p,q)$ 可以表示为 $(xl+dx\times k,yr+dy \times (cnt-1-k))$ 的形式，其中 $dx,dy$ 分别是 $x$ 和 $y$ 坐标的等差，$cnt$ 是线段上的二元组的个数。那么如果 $\lfloor \frac{X-mid\times xl}{dx} \rfloor + \lfloor \frac{Y-mid\times yr}{dy} \rfloor \ge mid \times (cnt-1)$ 显然是可以凑出 $mid$ 对二元组的。

9.8

AGC 044

A - Pay to Win

xjb 记忆化一下就能过了。

可以发现状态都是形如 $\lceil \frac{n}{2^x 3^y 5^z} \rceil$ 或者 $\lfloor \frac{n}{2^x 3^y 5^z} \rfloor$ 形式，所以复杂度是对的。

B - Joker

每次暴力更新最短路就行，冷静分析一下可以发现复杂度是三次的。

C - Strange Dance

倒着建 Trie 就行了。

D - Guess the Password

可以发现询问形如 AAAABBBB 形式的串会返回前半部分不是 A 的字符个数加上后半部分不是 B 的字符个数，相当于知道前半部分 A 的个数和后半部分 B 的个数的和。

考虑分治，对于区间 $[l,r]$，对于每种存在的字符 $B$，询问前半部分全是某种存在的字符 $A$ 和后半部分全是当前的字符，可以得到 $[l,mid]$ 中 $A$ 的个数加上 $[mid+1,r]$ 中 $B$ 的个数，我们把所有这些询问得到的值加起来，其实这个值就等于 $[l,r]$ 存在的种类数倍的 $[l,mid]$ 中 $A$ 的个数加上 $r-mid$，于是我们可以得到 $[l,mid]$ 和 $[mid+1,r]$ 中所有字符的个数。

注意分治的过程中还要随便维护下字符个数的在前缀的出现个数和在后缀的出现个数。

E - Random Pawn

先考虑一个弱化版。

大概是去掉了环和 $B$ 的限制。

考虑棋子的决策，肯定是一直走，直到走到一个点使得走不如留下更优。

于是我们只需要找到哪些点是终止点。

首先有一个结论：在长度为 $L$ 的数轴上的位置 $x$ 处，每次进行左右移动（左右概率都为 $\frac{1}{2}$），若到达 $0$ 或 $L$ 即停止，则到达 $0$ 停止的概率为 $\frac{L-x}{L}$，到达 $L$ 停止的概率为 $\frac{x}{L}$。

关于这个结论的证明，考虑设在 $i$ 开始，到 $L$ 停止的概率为 $F_i$，则 $F_i=\frac{F_{i-1}+F_{i+1}}{2}$，所以不难发现 $F$ 是个等差数列，又因为 $F_{0}=0,F_{L}=1$，所以上面的结论得证。

加入从 $i$ 出发，左边第一个终止点是 $a$，右边是 $b$，则当前点走的收益是 $E=v_a\times \frac{b-i}{b-a}+v_b\times \frac{i-a}{b-a}$，这个式子化一下，可以发现其实就是直线 $x=i$ 和两端分别是 $(a,v_a),(b,v_b)$ 的线段的交点的纵坐标。

冷静分析一下，不难发现终止点都位于上凸包上面。

现在考虑加上环和 $B$ 的限制咋做。

环可以先把 $\max$ 移到开头，把环转化成链，因为 $\max$ 肯定是个终止点。

对于 $B$ 的限制，考虑把 $B$ 消掉。

首先转移长这样：

\[E_i = \max(A_i,\frac{E_{i-1}+E_{i+1}}{2}+B_i)\]

考虑消掉 $B_i$，我们可以构造一个 $C$ 来干掉 $B$。

\[E_i-C_i = \max(A_i-C_i,\frac{E_{i-1}+E_{i+1}-C_{i-1}-C_{i+1}}{2}+\frac{C_{i-1}+C_{i+1}}{2}+B_i-C_i)\]

$C_i$ 需要满足 $B_i=\frac{C_{i-1}+C_{i+1}}{2}-C_i$。

可以令 $C_1=C_2=0,C_{i+1}=2(B_i+C_i)-C_{i-1}$。

令 $F_i = E_i-C_i,G_i = A_i - C_i$。

转移就变成了：

\[F_i = \max(G_i,\frac{F_{i-1}+F_{i+1}}{2})\]

可以发现这就转化成了弱化版。

F - Name-Preserving Clubs

可以看这里或者官方题解。

9.9

Hitachi 2020

C - ThREE

按深度奇偶性分组，每对距离为 $3$ 的两个点不会出现在同一个组。

如果个数少的那个组比 $\bmod \ 3=2$ 的数多，就分别先放 $\bmod \ 3\ =2$ 和 $\bmod \ 3=1$ 的数，然后把多出来的数改成 $3$ 的倍数，不然 $3$ 的倍数个数肯定比少的那个组的个数多，可以先把少的那个组填满 $3$ 的倍数，剩下的数全扔到另外一个组就行了。

D - Manga Market

显然 $a\ne 0$ 的店只会逛 $O(\log)$ 个。

可以先贪心给这些 $a\ne 0$ 的店排序（大概类似国王游戏那个题），然后 dp 一下。

枚举下 $a=0$ 取几个，答案随便算算就行。

E - Odd Sum Rectangles

随便打打表找找规律就行。

先把整个矩阵全设成 $1$。

每次把正中间的点设成 $0$，然后分治左上角右上角左下角右下角就行。

具体证明可以看官方题解。

F - Preserve Diameter

首先可以发现 $H$ 的直径是唯一的，否则显然可以继续加边。

设这条直径两个端点为 $s,t$，考虑建出任意一棵以 $s$ 为根的 BFS 树，令 $dep_i$ 表示 $i$ 在 BFS 树上的深度，那么两个点 $u,v$ 在 $H$ 中有边必须满足 $|dep_u-dep_v|\le 1$。

注意到所有直径的中点为同一个点，先考虑中点唯一的情况，设这个中点是 $mid$。

考虑以 $mid$ 为根再建出一棵 BFS 树，给每个点重新求一个 $dep_i$，满足：

$dep_{mid}=0$。
恰好存在一个点 $x$ 满足 $dep_x=-\frac{L}{2}$。
恰好存在一个点 $y$ 满足 $dep_y=\frac{L}{2}$。
对于在 $G$ 中有边的点对 $(u,v)$，满足 $|dep_u-dep_v|\le 1$。

其中 $L$ 表示直径长度。

可以发现一个合法的 $H$ 一定恰好对应两种满足以上条件的标号方案。

于是我们可以 DP，状态需要记当前子树目前满足第二个条件的点的个数（和 $2$ 取 $\min$）和满足第三个条件的点的个数（和 $2$ 取 $\min$），转移枚举当前的边的取值（$\{-1,0,1\}$）就行。

$L$ 为奇数时类似，只需要将直径中间的边断开后对两边分别 DP 后合并即可。

Keyence Programming Contest 2020

D - Swap and Flip

可以发现一张牌最后最终哪面朝上和它移动的距离奇偶性有关。

考虑从前往后 dp，令 $dp_{i,j,k}$ 表示位置 $i$ 放了 $j$ 号牌，前 $i$ 个位置放了哪些牌。

注意算距离的时候用逆序对算就行了。

E - Bichromization

直接给一个构造方案吧。

把每条边的边权设置为 $\max(d_{u_i},d_{v_i})$。

$d_i$ 相同的连通块可以直接一次 dfs 黑白染色。

按 $d_i$ 从小到大处理连通块，每次直接随便选一个比当前连通块的 $d_i$ 小的连通块，两个连通块之间相连的点颜色不同就行。

最后构造完判下 -1 就行。

F - Monochromization

先考虑一开始全白怎么搞。

考虑什么样的一个矩形能被操作到。

显然每次一直删除一行一列全一样的，如果全删完了就能得到。

考虑根据这个东西 dp，令 $f_{i,j,0/1}$ 表示删到 $i \times j$，最后一次删了行，删的行颜色是不是全一样的。

$g_{i,j,0/1}$ 同理，只是行换成了列。

为了防止算重，我们在删除的时候要做到尽量能删就删，转移也是据此设计的。

$f_{i,j,0}=\sum_{k=1}^{n-i} \binom{i+k}{k} \times g_{i+k,j,0}\times (2^k-2)$

$f_{i,j,1}=\sum_{k=1}^{n-i} \binom{i+k}{k} \times (2\times g_{i+k,j,0}+g_{i+k,j,1})$

$g$ 的转移也是类似的。

算答案就枚举枚举不去动哪些行和哪些列，需要保证这些不去动的行/列不能再删了，然后统计它们对答案的贡献。注意统计过程中需要再除掉组合数，因为删去的行和列都已经钦定了。

9.11

AGC 043

A - Range Flip Find Route

如果确定了一条从起点到终点路径，最小操作数就是这段路径经过了几段 #，根据这个 dp 就行了。

B - 123 Triangle

考虑只有 0 和 1 怎么做。

每次操作可以看做是把 $x_i$ 改成了 $(x_i+x_{i+1}) \bmod \ 2$，所以每个 1 对最终的数的贡献就是一个组合数 $\bmod \ 2$，可以直接卢卡斯定理算。

只有 0 和 2 是一样的。

如果三种都有，可以发现其实 2 可以看做是 0，可以证明最终答案肯定不是 2。

C - Giant Graph

$O(n^3)$ 的贪心大家都会，问题在于怎么优化。

仔细观察判断每个点能否选的式子，可以发现这好像长得像个博弈的模型。

多维的情况就是每一维 xor 起来，可以算出每个图的每个点 sg 函数，最后暴力合并。

可以证明 sg 函数的值域是 $O(\sqrt{m})$ 的。

D - Merge Triplets

在元素两两不同的归并排序中，结果等价于将所有序列按照前缀最大值划分之后，按照块头大小排序得到的序列。

所以就是要数满足能划分成大小为 $1,2,3$ 的块，且能拼成 $n$ 个大小为 $3$ 的块的排列个数。

能拼成 $n$ 个大小为 $3$ 的块也就是大小为 $1$ 的块的个数不能比大小为 $2$ 的块的个数少。

对于一个划分，方案数为 $\frac{N!}{\prod_{i=1}^{m}(\sum_{j \le i} siz_j)}$。

dp 的时候记一下大小为 $1$ 的块的个数和大小为 $2$ 的块的个数的差就行了。

E - Topology

首先有一个结论：

过每个点作一条关于 $x$ 轴的垂线，从绳子的最左端开始，沿绳子指定一个方向行进，穿过第 $i$ 条线上方的时候记录一个 $u_i$，穿过第 $i$ 条线下方的时候记录一个 $d_i$，这样游走得到一个字符串，不断地在字符串中选择两个相邻且相同的字符删掉，如果能清空，则该点集合法，否则非法。

每次删除两个相同字符说明可以把绳圈的一部分拉过来，能清空说明能完全分离。

先把无解判了，考虑怎么构造。

考虑对于一个不存在子集不合法的集合 $S$，构造一个经过 $(0,1)$ ，$S$ 不合法，$S$ 所有子集都合法的圈。最后把所有圈在 $(0,1)$ 相连。

考虑如下递归构造，当前处于所有点最左侧。

只有一个点，绕个圈就行了，$ans= u_1d_1$。
否则 $ans=u_i+ans+u_i+d_i+\text{reverse}(ans)+d_i$。

正确性显然。

长度上界是 $4n \times 3^n$，实际常数很小。

F - Jewelry Box

先考虑单组询问。

考虑如何判断一个选择的方案是否合法。

显然我们对于每家店的商品按 $siz$ 排序后按顺序选，然后 check 是否合法就行。

所以一对 $(u,v,w)$ 的限制就等价于，对于 $u$ 商店，$\le S_{u,i}$ 的商品买了 $a$ 个，则 $v$ 商店 $\le S_{u,i}+w$ 的商品至少买 $a$ 个。

用 $x_{i,j}$ 表示商店 $i$ 前 $j$ 轻的商品买了多少个。

容易发现这是一个线性规划问题：

限制是：

\[x_{i,K_i}-x_{i,0}=A\]

\[x_{i,j}-x_{i,j-1} \le 0\]

\[x_{i,j-1}-x_{i,j} \le -C_{i,j}\]

\[x_{v_i,j}-x_{u_i,k} \le 0\]

需要最小化：

\[\min(\sum_{i,j} (x_{i,j}-x_{i,j-1})P_{i,j})=\min(\sum_{i,j}x_{i,j}(P_{i,j}-P_{i,j+1}))\]

对偶一下，令上面几个限制对应的变量分别是 $a_i,b_i,c_{i,j},d_{i,j},e_{i,j}$。

则限制为：

\[-c_{i,1}+d_{i,1}-a_i\le -P_{i,1}\]

\[c_{i,K_i}-d_{i,K_i}+a_i\le P_{i,K_i}\]

\[c_{i,j}-c_{i,j+1}-d_{i,j}+d_{i,j+1}+\sum e_{k,l}-e_{p,q} \le P_{i,j}-P_{i,j+1}\]

需要最大化：

\[\max(\sum a_iA-d_{i,j}C_{i,j})\]

把几个限制的左右加起来可以发现都能消掉，所以几个限制不等号肯定是等号，再稍微调整下式子：

\[-(c_{i,1}-P_{i,1})+d_{i,1}-a_i=0\]

\[(c_{i,K_i}-P_{i,K_i})-d_{i,K_i}+a_i=0\]

\[(c_{i,j}-P_{i,j})-(c_{i,j+1}-P_{i,j+1})-d_{i,j}+d_{i,j+1}+\sum e_{k,l}-e_{p,q} = 0\]

可以把每个限制看做是一个点，每条边是一个变量建图，每个点流量汇入和流出的平衡就相当于等式成立。

可以发现这是一个最小费用循环流问题。

对于 $c_{i,j}$ 可以把 $c_{i,j}-P_{i,j}$ 看成一个整体，所以 $c_{i,j}$ 的取值变成了 $[-P_{i,j},+\infty)$，只需要 $(i,j)$ 向 $(i,j-1)$ 连 $P_{i,j}$ 的边，反过来连 $\infty$ 的边即可。

注意到这个图的环肯定是从 $S$ 流向 $T$，再从 $T$ 通过 $A$ 边权的那条边回来，于是我们可以把那条边先搞掉，对于剩下的图跑费用流，对于每个流量记一下对应费用，由于费用流的凸性，最后可以二分得到跑了前几圈从而得到答案。

9.14

AGC 041

A - Table Tennis Training

距离是偶数就直接往两者中间走，不然先走到两端等一局再往中间走。

B - Voting Judges

考虑怎么判断一个数 $a_i$ 能否合法。

一开始就在前 $p$ 名显然合法。

加上 $m$ 还是挤不进去前 $p$ 名肯定不合法。

显然 $m$ 次操作都会选择 $a_i$，另外我们可以先钦定 $p-1$ 个数在最终比当前的数大，那么这些数每次操作也都会选上，接下来就是判断把剩下的数搞出一个 $a_i+m+1$ 需要的操作数和剩下的操作数的大小关系。

那显然我们会贪心的选择钦定前 $p-1$ 名的数每次都选。

剩下的每个数 $a_j$ 能填的操作数就是 $\min(m,a_i+m-a_j)$。

C - Domino Quality

先手玩出 $3,4$ 的情况然后判掉。

可以手玩出 $5,6,7,8,9$ 每行每列都是三个的方案。

然后每次把 $n$ 行分成左上角 $\lceil \frac{n}{2} \rceil \times \lceil \frac{n}{2} \rceil$ 和右下角 $(n-\lceil \frac{n}{2} \rceil) \times (n-\lceil \frac{n}{2} \rceil)$ 的情况，所以要手玩到 $9$...

D - Problem Scores

限制条件推一推就可以得到就是要数满足以下条件长度为 $n$ （先假设 $n$ 为奇数，偶数情况类似）的序列个数：

$\forall i,a_i\in [1,n]$
$\forall i \in [1,n),a_i \le a_{i+1}$
$\sum\limits_{i=1}^{\frac{n+1}{2}} a_i > \sum\limits_{i=\frac{n+3}{2}}^{n} a_i$

直接 dp 原序列有点难搞，我们可以 dp 这个序列的差分数组。

问题转化为有重量为 $1,0,-1,-2,-3, \ldots ,-k$ 的物品，每种物品有无限个，求选择不超过 $n$ 个使得重量和为正整数的方案数。

考虑把一个重量为 $-k$ 的物品和 $k$ 个 $1$ 捆绑，于是只要 dp 数量就行了。

E - Balancing Network

$T=1$ 考虑从前往后考虑每个平衡器，对于每条线用 bitset 维护下能跑到这条线的线，对于当前平衡器 $(a,b)$，$a$ 和 $b$ 两条线的 bitset 变成两者的并就行了。

找到一条所有线能跑到的线从后往前构造就行了。

$T=2$ 考虑从后往前考虑每个平衡器，对于每条线 $i$ 记一下 $i$ 最终跑到哪条线和跑到 $i$ 有多少条线，目标是不存在一条线能跑到这条线的个数为 $n$，对于当前平衡器 $(a,b)$，要么 $a$ 跑到了 $b$ 最终跑到的线，要么 $b$ 跑到了 $a$ 最终跑到的线，显然存在一种方案使得满足条件，因为当 $n>2$ 的时候不会同时存在两个 $n-1$。

F - Histogram Rooks

考虑从高往低 dp，具体来说就是建笛卡尔树然后从下往上合并，直接 dp 需要记上面有几列放了以及有几列有格子空着。

要记两维是因为当前行一个都不放的时候，有格子空着的列数会变成当前行的长度减去上面有几列放了的个数。

于是单独处理这种情况状态就能改成一维了。

令 $f_{i,j}$ 表示 $i$ 子树有 $j$ 列放了的方案数，$g_{i,j}$ 表示 $i$ 子树有 $j$ 列有格子空着的方案数。

这一行一个都不放就是从 $f_{i,j}$ 转移到 $g_{i,len-j}$， $f$ 转移到 $f$ 枚举另外填了几列，$g$ 转移到 $g$ 枚举有格子空了的列填了几列就行了。

复杂度是 $O(n^3)$，可以用 FFT 优化到 $O(n^2\log n)$，并没能吊打标算。

9.15

Dwango Programming Contest 6th

A - Falling Asleep

xjb 枚举一下。

B - Fusing Slimes

对于每个间隔考虑贡献，对于 $x_i$ 和 $x_{i+1}$ 之间的间隔，原先前 $i$ 个数剩 $j$ 个的时候，有 $\frac{1}{j}$ 的概率贡献 $1$，所以 $x_i$ 和 $x_{i+1}$ 之间的间隔对答案的贡献是：$(x_{i+1}-x_i)\times \sum_{j\le i}\frac{1}{j}$。

考虑组合意义，$\prod_{i} c_i$ 相当于每个孩子还要从他的曲奇里选一个。

考虑根据这个 dp，令 $dp_{i,j}$ 表示前 $i$ 天有 $j$ 个孩子选到了曲奇。

转移枚举当前天另外有几个孩子选到了曲奇，然后剩下的曲奇随便分就行。

D - Arrangement

考虑从前往后贪心放。

设没被 ban 的最小值为 $x$。

分三种情况讨论：

存在一个数 $i$，使得还没放所有 $j$，$a_j=i$ 这个时候我们只能放 $i$，不然就会不合法。
放 $x$ 之后还剩两个数 $p,q$，并且 $a_{p}=q,a_{q}=p$，这个时候放 $x$ 会不合法，$p,q$ 中选一个没被 ban 的放。
放 $x$。

E - Span Covering

先套一层容斥。

先把答案的式子写下：

\[\sum_{T} (-1)^{|T|} \prod_{i} \sum_{j,\ l_j\ge L_i} l_j-L_i+1\]

稍微改下：

\[\sum_{T} (-1)^{|T|} \prod_{i} ((\sum_{j,\ l_j\ge L_i} l_j)-(\sum_{j}[l_j\ge L_i]\times (L_i-1))\ )\]

考虑从大往小 dp，可以发现贡献只和 $\sum_{j}{l_j}$ 和 $\sum_j{1}$ 有关，状态只要记这两维就行了。

最后转移的时候还要乘一下组合数。

稍微分析一下可以得到复杂度是 $O(X^3)$ 的。

DISCO Presents Discovery Channel Code Contest 2020 Qual

A - DDCC Finals

随便算算。

B - Iron Bar Cutting

随便算算。

C - Strawberry Cakes

随便构造。

D - Digit Sum Replace

注意到怎么删次数都是一样的，于是随便算算。

E - Majority of Balls

如果找到了 $\frac{N-1}{2}$ 个蓝球和 $\frac{N-1}{2}$ 个红球，剩下的随便问问就行。

注意到一定存在一个区间满足这个条件，于是二分一下就行了。

F - DISCOSMOS

首先可以转化到 $T=1$ 的情况。

对于 $T=1$ 的情况可以打表找一波规律。

不难发现答案是 $2^n+2^m-1+2^{\gcd(n,m)}-2$。

9.16

AGC 040

A - ><

模拟。

B - Two Contests

一个集合的交是 $\min{r}-\max{l}+1$。

分成两个集合的话一个集合的 $\max l$ 是确定的，枚举另一个的 $\max l$，设为 $k$，最终 $k$ 所在集合要么是只有一个区间要么就是所有 $l \le k$ 的区间。

C - Neither AB nor BA

首先可以黑白染色，偶数位置的 $A,B$ 取反，限制转化为不能删除 AA 和 BB。

可以发现这样一个合法的字符串需要满足的是 $\max(cntA,cntB) \le \frac{n}{2}$，用合法方案减去不合法方案就行。

D - Balance Beam

对于一种排列，显然能 win 的是一个前缀。

画出两者的图像，$x$ 是距离，$y$ 是时间，显然两者的图像由 $n$ 条折线组成，如果这两条折线有交则说明能 win。上下移动第二个玩家的折线，使得两者折线的交只有一个点，此时第二个玩家与 x 轴的交点 $(k,0)$ 就是最后一个能 win 的点，我们的目标就是最大化这个 $k$。

枚举 $(k,0)$ 对应的是哪条线段，设为 $p$，考虑这样一条折线：从 $(k,0)$ 出现，先沿着第二个玩家的折线向上走，走到两者交点就沿第一个玩家的折线走，最终会走到 $(n,s)$，其中 $s=\sum_{i} a_i$。容易发现每一种方案一定可以找出这样一条折线，并且这条折线能对应一种方案。要最大化 $p$ 也就是走过的线段要尽量少，也就是这些线段要尽量陡。

于是我们贪心地选择 $\max(a_i,b_i)$ 最大的那些线段放到 $p$ 后面，并且这个上界是可以达到的，只要把 $a_i<b_i$ 的放在两折线交点前面，其他的放在交点后面即可。

于是我们只要二分出，取前多少个线段能使得 $\sum_{i} \max(a_i,b_i) \ge s-b_p$，小数部分特殊算算就行。

E - Prefix Suffix Addition

设 $x_i$ 表示第 $i$ 个数通过第二种操作增加的值，$y_i$ 为第一种操作增加的值，$\forall i,x_i+y_i = a_i$，需要的操作数则为 $\sum_{i} [x_i>x_{i-1}]+[y_{i+1}<y_i]$。

考虑一个一个贪心，不难发现对于代价相同的方案，$x_i$ 小的一定更优，并且对于代价比当前最优方案代价要大至少 $2$ 的方案，它一定不会更优。

于是我们只要记最优解和次优解就行。

F - Two Pieces

考虑用 $(p,q)$ 来表示一个点，其中 $p $表示较远的点的坐标，$q$ 表示两者的距离。

有三种操作：

$p,q$ 同时加一。
$q$ 减一，但此时要满足 $q\ge 2$。
将 $q$ 清零。

考虑确定前两个操作序列，然后插入第三种操作算方案。

不难发现第一种操作会恰好执行 $B$ 次，枚举第二种操作次数，设为 $k$。

如果 $n=B+k$，直接折线法算算就行。

否则考虑插入第三种操作，可以发现插入的第三种操作必须满足以下两个条件：

最后插入的第三种操作必须插在最后一个 $q=A-k$ 的位置。
不会使得第二种操作不合法。

为了满足第二个条件，如果要在某个 $q=t$ 的位置后面插入一个第三种操作，那么这个位置后面不能出现 $q' \le t$ 的位置，也就是说可以在最后一次 $q=0,1,2,3,\dots,A-k$ 的位置后面可以插入任意个数的第三种操作。注意到确定第一种和第二种操作顺序和插入第三种操作是独立的。确定第一种和第二种操作顺序的方案数可以折线法，插入第三种操作可以隔板法。

9.17

AGC 039

A - Connection and Disconnection

长度为 $len$ 的连续段需要替换 $\lfloor \frac{len}{2} \rfloor$ 个。

注意头尾连续段如果字符相同且长度都为奇数还需要额外替换一些。

B - Graph Partition

如果存在奇环则无解。

否则求下直径就行了。

C - Division by Two with Something

先定义一个二进制数存在一个长度为 $d$ 的循环节需要满足以下条件：

$d$ 是 $n$ 的一个因子，且 $\frac nd$ 是奇数。
$\forall i \in [d+1,n], x_i\ne x_{i-d}$。

打表找规律可以发现，一个数最短的循环节如果长度为 $len$，那么这个数对答案的贡献是 $2\times len$。

从小到大对每个合法的长度 $d$ 求一下存在一个长度为 $d$ 的循环节且满足限制的数的个数，然后减去最短循环节小于 $d$ 且是 $d$ 的因子的数的个数就行。

D - Incenters

考虑单位圆上 $\Delta ABC$，取这三段弧的中点，分别记为 $A',B' ,C'$。

首先，$\Delta ABC$ 的内心和 $\Delta A'B'C'$ 的垂心是一样的。

然后，根据欧拉线的知识，$\Delta A'B'C'$ 的垂心就是三个点的坐标和。

于是对每对点算贡献就行了。

E - Pairing Points

先枚举 1 和谁连，圆被分成了两半。

记 $f_{l,r,L,R}$ 表示区间 $[l,r]$ 和区间 $[L,R]$ 中的点配对的方案。

可以发现配对方案一定是在 $[l,r]$ 中选一些点 $x_1,x_2,\dots,x_m(x_i<x_{i+1})$ 和 $[L,R]$ 中选一些点 $y_1,y_2,\dots,y_m(y_i>y_{i+1})$，然后 $x_i$ 和 $y_i$ 配对，再然后是 $[l,r]$ 和 $[L,R]$ 中的点自己配对。

我们可以据此设计转移，另外为了防止算重，我们再记 $g_{l,r,L,R}$ 表示区间 $[l,r]$ 和区间 $[L,R]$ 中的点配对，$[l,r]$ 中的点和 $[L,R]$ 中的点配的只有一对。

考虑枚举最后一对 $(x_m,y_m)$ 所在区间：

$f_{l,r,L,R}=\sum_{i,j} f_{l,i,j,R}\times g_{i+1,r,L,j-1}$

$g$ 的转移就枚举配的那对点就行：

$g_{l,r,L,R}=\sum_{i,j} f_{l,i-1,i+1,r}\times f_{L,j-1,j+1,R}$

复杂度是 $O(n^6)$ 的，但是常数小的一批。

F - Min Product Sum

首先有一个显然错误的计算方式，如果每行每列钦定了最小值 $a_i,b_j$，那么这种情况的价值是 $\prod_{i,j} \min(a_i,b_j)$，方案数是 $\prod_{i,j} (k+1-\max(a_i,b_j))$。

但是我们可以套一层容斥让这种方式正确。

考虑 dp 这个东西，令 $f_{i,j,k}$ 表示填到 $k$，已经填满了 $i$ 行 $j$ 列。

转移考虑枚举加入的不被容斥的行数、不被容斥的列数、容斥的行数、容斥的列数，但这样复杂度很高，我们可以依次枚举这些东西转移，时间复杂度就优化到了 $O(knm(n+m))$。

9.19

NIKKEI Programming Contest 2019-2

C - Swaps

显然 $A,B$ 分别排序后，如果存在一个位置 $A_i>B_i$，则无解。

$N-1$ 次操作显然可以把整个序列排序，而 $N-2$ 次操作相当于是再交换一对 $(i,j)$ 则可以把整个序列排序，所以如果存在 $A_i\le B_{i-1}$，显然肯定有解。

另外还有就是 $N-2$ 次操作就能把整个序列排序，也就是排列的置换环不止一个。

D - Shortest Path on a Line

每个 $(L,R,C)$ 可以看做是 $[L,R]$ 向 $R$ 连了一条边权为 $C$ 的边。

从前往后一个一个算就行。

E - Non-triangular Triplets

如果 $\sum_{i=K}^{K+2N-1} i > \sum_{i=K+2N}^{K+3N-1} i$ 就无解，否则肯定有解。

直接给出构造方法吧，可以证明当上面条件满足的时候这样构造肯定是对的。

$\forall i \in [1,\lceil \frac{n}{2} \rceil ]$，$k+i-1$ 和 $k+n+\lfloor \frac{n}{2} \rfloor+i-1$ 配对。

$\forall i \in [\lceil \frac{n}{2} \rceil+1,n]$，$k+i-1$ 和 $k+n+i-1$ 配对。

按照 $a+b$ 的和从小到大和 $[K+2N,K+3N-1]$ 配对就行。

F - Mirror Frame

一个环上的点 $x+y$ 的奇偶性是相同的，奇偶性相同的环才会有交点，于是独立的，另外两个环的四个交点肯定是一样的。

考虑一个完全图 $G$，图中每个点代表原图的每一个环，每条边代表这两个环的交点。

则一次操作相当于选择一条边，反转边的两个端点相邻的边的状态。

目标是把边置为 $0$。

考虑确定了边的状态后怎么判断是否存在一种操作的方案。

如果操作一个环上的所有边，则会使环上所有边状态反转，环外所有边状态不变，也就是说，存在合法方案的充分条件为图中的 open 边存在欧拉回路。

点数是偶数肯定有解，如果我们翻转两个点 $(a,b)$ ,那么 $a,b$ 相邻的 $1$ 边度数的奇偶性发生变化,所以可以通过操作使得所有点的度数为偶数.所以当 $n$ 为偶数的时候一定合法。
点数是奇数，那么存在操作方法的条件是只考虑状态为 open 的边时，所有点的度数都是偶数，因为翻转两个点 $(a,b)$ 时, $a,b$ 的度数奇偶性不会发生变化。

统计方案考虑每个不确定的边的连通块，open 边度数为奇数的点必须是偶数个，否则无解，另外只要考虑搞出一棵生成树，生成树以外的边随便选，最终可以调整生成树上的边，方案数就是 $2^{m-(n-1)}$。

Japanese Student Championship 2019 Qualification

C - Cell Inversion

考虑差分，每个位置最终是选为左端点还是右端点可以确定。

判下无解后，随便算算方案就行了。

D - Classified

对于一个颜色的边组成的图必须是个二分图，于是每次把图分成两半，两两之间的边为同一个颜色，然后递归下去做就行。

E - Card Collector

考虑我们现在选了一些点，怎么判是否存在一种拿的方案、

考虑这样一个图，行列是图中的 $H+W$ 个点，每个选择的数 $(x,y)$ 相当于 $x$ 向 $H+y$ 连一条边。

那么存在一种方案就相当于存在一种匹配使得每条边能恰好和一个端点匹配，每条边和每个点都只能匹配一次。

稍稍画个图想想就能发现，一个连通块最多只能允许存在一个环，也就是说如果这个图是基环树森林就是合法的。

于是我们考虑从大到小考虑每个点，如果加入合法就加入这个点。

具体维护可以用并查集。

正确性可以用拟阵证。

F - Candy Retribution

考虑用合法方案减去不合法方案。

也就是存在一个 $x$ 使得前 $m$ 大的数大于等于 $x$，而剩下的数小于 $x$。

枚举这个 $x$，容斥计算方案就行。

9.21

AGC 038

A - 01 Matrix

左上角是 $b\times a$ 的全 1 矩阵，右下角是 $(n-b)\times (m-a)$ 的全 1 矩阵就行。

B - Sorting a Segment

可以发现分别对两个区间排序后是否长一样和被 sort 到的第一个数和最后一个数有关。

于是正着倒着分别做一遍找到每个区间 sort 到的第一个数和最后一个数就行，set 或者单调队列维护就行。

C - LCMs

随便推推式子就行了。

D - Unique Path

显然 $0$ 边的连通块不能存在一个 $1$ 边。

把 $0$ 边的连通块可以看成一个点，为了解决 $1$ 边，至少需要把这些点连成一个环，至多可以连成完全图。

判下 $m$ 是不是在那个区间内就行。

注意判下不存在 $1$ 边。

E - Gachapon

考虑先套一层 Min-Max 容斥，枚举每一个子集，计算其中存在一个满足要求时步数期望，考虑转化为求 $i$ 次还没达到条件的概率之和。

也就是对于每一个未结束的局面要算出到达该局面的概率，该局面对于答案的贡献是概率乘上保持该局面的概率。

写一下一个未结束的局面的贡献的具体式子，大概是 $\dfrac{(\sum x_i)!}{\prod x_i!}\times \prod p_i^{x_i}$，其中 $x_i$ 表示 $i$ 被随到的次数，$p_i$ 表示在这个集合中选出 $i$ 的概率，少写了容斥系数和保持该局面的概率，但是没有影响。不难发现只和 $\sum{a_i}$ 和集合内的点被随机到的总次数之和有关，于是 dp 的时候只要记这两维就行了，容斥系数可以在 dp 的时候乘进去，保持该局面的概率可以在最后乘。

可以证明复杂度是 $O((\sum a_i)(\sum b_i)^2)$ 的。

F - Two Permutations

先转化为求 $\min(\sum_{i} [A_i=B_i])$。

不难发现一个置换环要么是转动一次 $(A_i=P_i)$，要么不转动 $(A_i=i)$。

考虑这样一个最小割模型，$P$ 和 $Q$ 中的大小大于 $1$ 的环是图中的点。

$P$ 中的一个环 $p$ 如果最终归到 $S$ 集，表示 $p$ 转动了，否则表示 $p$ 没转。

$Q$ 中的一个环 $q$ 如果最终归到 $S$ 集，表示 $q$ 没转，否则表示 $p$ 转动了。

可以发现如果两个有交的环 $p,q$ 最终归到同一个集合，这两个点之间是不会产生任何贡献的，因为一个没转一个转了，而两者的大小都大于 $1$，也就是不存在 $P_i=i$，此时的贡献应该是不转的那个集合对应的自环的个数。

如果两者归到同一个集合，可以发现贡献要么是两者对应的自环个数之和和两者交的大小，要么是两者的交 $P_{x_i}=Q_{x_i}$ 的个数。

于是根据这个建图就行。

可以发现这个图是个二分图，众所周知二分图跑 Dinic 复杂度是 $O(m\sqrt n)$ 的。

9.22

AGC 037

A - Dividing a String

如果不能分出一个就分出两个，判一下最后末尾分不出来就要合并最后两个串。

B - RGB Balls

每个点是三元组的哪个位置可以确定，于是随便算算方案就行了。

C - Numbers on a Circle

考虑倒着做就完事了。

D - Sorting a Grid

把最终矩阵的所有第 $i$ 行的数看成是 $i$ ，第一步相当于是排列行，使得每一列是个排列。

考虑一列一列做，每次是一个二分图匹配。

正确性可以用 Hall 定理证。

E - Reversing and Concatenating

前 $k-1$ 次取倒过来后字典序最小的串，最后一次取字典序最小的串。

显然当 $k>n $ 的时候答案是长度为 $n$ 由原字符串最小字符组成的串。

直接做 $k$ 次，每次暴力判断两个串的字典序的话复杂度就是 $O(n^2\log n)$ 的，但还是跑的飞快。

可以用二分+哈希或者后缀数组优化到 $O(n\log n)$，但没啥必要。

F - Counting of Subarrays

考虑一个序列怎么判是否合法。

要么长度为 $1$，要么每次取出最小的数 $x$ 构成的连续段，合成尽量多的 $x+1$，最后能合成一个大于 $\max$ 的数。

维护所有值域相同的连续段，每次取出值最小的段，合并成 $x+1$，并计算方案。

为了算方案，我们需要维护每个点分别表示一个数充当左端点的方案数与一个数充当右端点的方案数，分别记为 $lv_i$ 和 $rv_i$。

对于一个区间 $[l,r]$，$[l,l+L)$ 显然无法充当右端点，$[l+L,l+2L-1]$ 可以充当第一个 $x + 1$ 的右端点，将所以第一个 $x+1$ 的 $rv$ 为 $\sum_{i=l+L}^{l+2L-1} rv_i$，第二个 $x+1$ 的 $rv$，第三个 $x+1$ 的 $rv$.. 也是同理。

$lv$ 也是同理。

注意可能会算重，需要在 $x$ 合成 $x + 1$ 的过程中，减去 $x + 1$ 合成 $x + 2$ 产生的贡献。

具体实现可以用链表删减元素，用 set 取出最小 $x$。

9.23

diverta 2019 Programming Contest 2

C - Successive Subtraction

有负数答案就是所有数的绝对值之和，全正数就是除了最小值的数的和减去最小值，全负数同理，可以根据答案构造。

D - Squirrel Merchant

考虑一个贪心的想法，A 便宜肯定在 A 尽量买了后在 B 卖，B 便宜肯定在 B 尽量买了后在 A 卖。

考虑讨论有几种商品在 A 便宜，枚举便宜的商品在 A 买了几件就行，如果有三种的只要枚举其中两种就行，因为另外一种肯定是尽量买的。

E - Balanced Piles

考虑这是一个不断把 $\min$ 扔到 $\max$ 的过程，如果 $\min$ 有 $a$ 个那么把所有 $\min$ 扔到 $\max$ 的方案就是 $a!$。

考虑如果当前 $\max$ 不是 $H$，那么 $\max$ 肯定还会再往上扔，于是原本要这些 $\max$ 变成 $\min$ 再算的贡献现在算就行。

于是我们就有了一个 $O(n^2)$ 的做法，状态两维记得是 $\max$ 和 $\max$ 的个数。

再分析一下可以发现，我们其实也并不关心 $\max$ 有几个，因为只要有至少一个 $\max$ 在了，所有的数都能扔到 $[\max+1,\max+D]$，于是状态只要记一维 $\max$ 就行了，每次乘个 $\sum_{i=1}^{n} i!$ 的系数就行。

F - Diverta City

考虑增量法。

我们可以构造一个非常优秀的序列 $f=\{1,2,4,7,12,20,29,38,52,73\}$，这个数列满足任意两个数字都不相同、任意两个数字的和也都不相同。

每次加入一个点 $i$ ，对于每个 $j\ (j<i)$ 连边权为 $(mx+1)\times f_j$ 的边，其中 $mx$ 为之前的哈密顿路长队的最大值。

每次新增加的哈密顿回路肯定比之前的长，并且两两不等，所以是对的。

M-SOLUTIONS Programming Contest

E - Product of Arithmetic Progression

把 $x$ 转化成 $kd$ 的形式。

F - Random Tournament

设 $F_{l,r,0/1}$ 表示只考虑区间 $[l, r]$ 中的人，$l / r$ 能否 win。

如果在区间 $[l,r]$ 中 $x$ 可以 win，可以发现 $[l,x]$ 和 $[x,r]$ 中的战斗是独立的，所以只要 $F_{l,x,1}=1$ 且 $F_{x,r,0}=1$ 即可。

暴力转移考虑枚举最后一次和 $l/r$ 打的 $x$，判断是否存在一个 $x$ 满足在少了 $l/r$ 的区间中能 win，并且 $l/r$ 能打过 $x$。

不难发现可以用 bitset 优化。

9.24

AGC 036

A - Triangle

第一个点选在 $(0,0)$，可以用叉积表示三角形的面积。

转化为构造四个非负整数 $a,b,c,d$ 满足 $ab-cd=s$。

令 $a=10^9,b=\lceil \dfrac{s}{10^9} \rceil,c=1,d=s-ab$ 就行。

B - Do Not Duplicate

令 $nxt_i$ 表示目前第一个数是 $A_i$ 下一次只剩一个数的时候那个数的下标。

显然不断加入 $X_i$ 就是一直从 $i$ 跳到 $nxt_i$ 的过程。

找出循环节后暴力做做就行。

C - GP 2

考虑一个序列是合法的需要满足下面三个条件：

$\max(a_i) \le 2m$
$\sum a_i = 3m$
$\sum [a_i \bmod 2=1] \le m$

注意到如果不满足第一个条件一定满足第三个条件。

于是可以用满足第二个条件和第三个条件的方案减去不满足第一个条件且满足第二个条件的方案。

D - Negative Cycle

考虑差分约束的模型，图中不存在负环等价于存在一组合法的差分约束的解。

考虑每个节点作为一个变量，第 $i$ 个节点对应的变量为 $x_i$。

令 $y_i=x_i-x_{i+1}$，由于边权都是 $1$ 或者 $-1$ 并且存在不能删的 $0$ 边, 显然 $y_i$ 值只能是 0 和 1 中的一个。

假设保留了一条边 $i \to j\ (i<j)$，就会有 $x_i-1\ge x_j$，也就是 $\sum_{k=i}^{j-1} y_k \ge 1$。

假设保留了一条边 $i \to j\ (i>j)$，就会有 $x_i+1\ge x_j$，也就是 $\sum_{k=i}^{j-1} y_k \le 1$。

于是就可以 dp 了，令 $f_{i,j}$ 表示最后两个 1 分别位于 $i,j$。

转移枚举下一个 1 放哪里，可以二维前缀和快速算需要删掉的边的边权和。

复杂度 $O(n^3)$。

E - ABC String

显然先可以去重。

设 $cntA,cntB,cntC$ 分别表示 $A,B,C$ 的个数，并且假设 $cntA\le cntB\le cntC$，为了最大化答案，我们希望删尽量少的 A，来使得三者相同。

首先先通过一些删除使得 $cntB=cntC$。首先可以把两边字符不同的 C，即左右是一个 A 一个 B 的 C 删掉，其实也就是删掉形如 ACBCB...BCA 的子串两边的 C，然后剩下的串每一段要么是 ABCB...CBA，这种类型 B 只能比 C 多 1 个，不可再更改；要么是 ACA，这我们可以删除第一个 A 和 C 来删除一个 C，可以发现我们只能通过删除这些 A 来让 $cntB=cntC$。

现在就是 $cntA\le cntB=cntC$。考虑删除形如 ABCBC..BCA 中间的若干对 BC 或者 ACBCB..CBA 中间的若干对 CB，需要注意的是删除完这些后两个 A 不能靠在一起。最后如果还有 A，则至少都有 ABCACBA...BCA，即两个 A 中间夹一个 BC 或 CB，这时有 $cntA > cntB = cntC$，所以删的过程中肯定存在一个时刻使得 $cntA=cntB=cntC$。

F - Square Constraints

每个位置能选的数显然是一个区间，设这个区间是 $[l_i,r_i]$。

首先如果没有 $l$ 的限制，将 $r$ 从小到大排序后，答案就是 $\prod_{i} (r_i-i+1)$。

考虑容斥掉 $l$ 的限制。

观察几个性质：

$\forall i \in [1,2n), l_i \le l_{i-1},r_i\le r_{i-1}$
$\forall i \in [n,2n), l_i=0$
$r_n\ge l_0$

如果暴力枚举了前 $n$ 个数每个数的限制，对所有限制排序就相当于是先归并 $[n,2n)$ 和 $[0,n)$ 中选了 $l$ 的那些限制，再在后面加上 $[0,n)$ 中选了 $r$ 的限制。

于是可以发现第 $i\ (i\in [0,n))$ 个数的限制如果选了 $l_i$，贡献是和 $[i+1,n)$ 中有几个数的限制是选了 $l$ 有关的；如果第 $i \ (i \in [0,n))$ 个数的限制选了 $r_i$，贡献是和 $[0,n)$ 中一共有几个数限制选了 $l$ 和 $[i+1,n)$ 中有几个数的限制是选了 $r$ 有关的。

于是 dp 的时候状态记这两维就行了。

令 $f_{i,j,k}$ 表示当前做到 $i$，$[i,n)$ 有 $j$ 个数选了 $l$ 的限制，$[0,n)$ 一共要有 $k$ 个数选了 $l$ 的限制。

每当 $i$ 移动的时候，双指针算算 $[n,2n)$ 的贡献。

转移就考虑当前点的限制是选 $l$ 还是选 $r$。

~~凑系数太痛苦了，建议直接找一个人的代码借鉴~~

复杂度是 $O(n^3)$ 的。

9.25

AGC 035

A - XOR Circle

可以发现 $a_i=a_{i+3}$。

所以不同的 $a_i$ 的值就三个，分情况判一下就行。

B - Even Degrees

边数为偶数肯定有解，否则肯定无解。

可以撸出一棵生成树，非树边随便选最后通过树边调整就行。

C - Skolem XOR Tree

显然当 $n$ 为 $2^k$ 时肯定无解，因为 $n$ 和 $2n$ 之间的路径的值不可能为 $n$。

考虑构造一棵以 $1$ 为根的类菊花树，把 $2k$ 和 $2k+1$ 分为一组然后这样构造。

\[ 2k - 2k+1 - 1 - 2k+1 - 2k \]

当 $n$ 为偶数的时候还会剩下一个 $n$，可以这样构造。

\[n-\text{lowbit}(n)\ \text{xor}\ 1 - 1 -n \ \text{xor} \ \text{lowbit}(n) - n\]

D - Add and Remove

考虑倒着做，每次插入一个最后删除的数。

可以发现这样原本的序列会被分成两个独立的区间，加入的数对答案的贡献和序列两边的数对最终的答案贡献次数有关。

于是状态记左右端点和左右端点对答案的贡献次数就行了。

可以证明复杂度是 $O(2^n\text{poly}(n))$ 的。

E - Develop

考虑一个删除序列是否合法，每个点 $i$ 往 $i-2$ 和 $i+k$ 连边，如果删除序列中的点有环则不合法，反之则合法。

如果 $k$ 为偶数，则编号为奇数的点和编号为偶数的点是独立的，分别随便 dp 算算就行。

如果 $k$ 为奇数，我们将奇数和偶数分别排开，得到了两条链，并把 $x$ 和 $x+k$ 放在同一层，那么一个不合法的环显然就是长先从左边往上走，然后走到右边，再往上走，最后再走回左边这样的。

于是就可以 dp 了，令 $f_{i,j,k}$ 考虑第 $i$ 层，往上然后往右再往上的路径长度为 $j$，右边链往上的路径长度为 $k$ 。

转移考虑当前层怎么选就行。

复杂度 $O(n^3)$。

F - Two Histograms

可以发现，这样的形状（见下图）有两种填的方法。

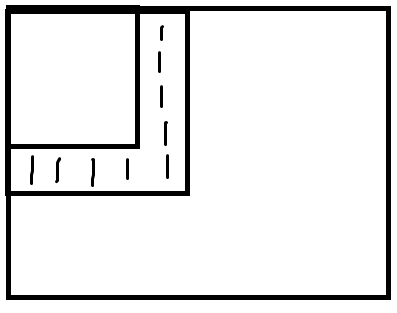
于是为了避免算重，对于上图的填充方式我们只取两种中的一种，也就是对于一种方案如果存在一对 $(x,y)$ 满足 $k_x=y-1,l_y=x$，那么这个方案就是不合法的；否则就是合法的。

可以发现一个网格唯一对应了一个合法方案，因为可以对一个网格的某一个方案，不停把不合法的操作调整成合法的操作，从而得到一个合法方案。所以直接考虑如何计数合法方案即可，这可以直接容斥，枚举 $k_x=y-1,l_y=x$ 的对数计算就行。

9.26

diverta 2019 Programming Contest

E - XOR Partitioning

先前缀和一下，可以发现一个合法的划分选的位置一定是 ..x..0..x..0 这样的形式。

对每个 $x$ DP 一下就行。

F - Edge Ordering

首先，一条非树边 $(u,v)$ 必须大于 $u \to v$ 这条链上的所有边。

考虑从大到小依次加入每条树边，则加入第 $i$ 条树边之前必须先加入第 $i$ 条树边控制的非树边。

每次加入的树边的权值必须是最小值，而非树边可以随便选。

问题在于如何统计答案。

设当前一共加入了 $n$ 条边，合法的序列种数 $c$，树边数为 $b$，和价值和为 $s$。

加入一条树边，这条树边的权值只能是 1，所以每种合法序列的每条树边权值会往后移动 1，所以 $(n,c,b,s)\to (n+1,c,b+1,s+(b+1)c)$

加入一条非树边，这条边的权值可以是 $[1,n+1]$ 中的任意一个数，先不考虑每条树边权值的移动，$s$ 会被计算 $n+1$ 次，可以发现对于一个合法序列 $p$，这条边的权值取遍 $[1,n+1]$ 中的所有数后，所有树边移动的权值和就是原先这个合法序列 $p$ 所有树边边权和，所以这一部分的贡献是 $s$，于是可以得到 $(n,c,b,s)\to (n+1,c(n+1),b,s(n+1)+s)$。

加入 $k$ 条非树边就是 $(n,c,b,s)\to (n+k,c(n+1)(n+2)\cdots(n+k),b,s(n+2)(n+3)\cdots(n+k+1))$

于是我们就可以 DP。

状态是哪些树边的边权已经确定，转移每次加入一条边就行。

本题不需要精密的实现，随便写个 $O(2^nm\alpha(n))$ 也能过。

Tenka1 Programmer Contest 2019

D - Three Colors

设 $A,B,C$ 分别表示三种颜色的数的和，$S$ 表示所有数的和。

根据小学知识，如果 $A,B,C$ 能够是一个三角形的三条边，需要满足任意两个数的和大于第三个。

我们用 $S-A-B$ 代替 $C$，把限制就是 $\max(2a,2b)\le S\le 2(a+b)$。

答案就是所有方案减去 $2(a+b)\le S$ 的方案和 $\max(2a,2b)\ge S$ 的方案，再加上 $2a=S=2(a+b)$ 的方案的三倍。

时间复杂度 $O(n^3)$。

E - Polynomial Divisors

可以发现当 $p>n$ 时需要满足所有系数都是 $p$ 的倍数。

$p\le n$ 暴力判判就行。

F - Banned X

先对整个序列前缀和一下，如果存在 $y$ 则不能存在 $y-x$。

如果我们知道整个序列不同的值有 $a$ 个，则可以用组合数算出对应的原序列的方案数。

可以发现如果首次在 $i$ 出现了 $i$ 和 $i+1$ 同时存在的情况，显然 $i<x-1$，则最多只能选到 $i+x-1$，并且 $x$ 到 $i+x-1$ 的选法唯一，$i+2$ 到 $x-1$ 可以随便选，枚举下 $i+2$ 到 $x-1$ 选了几个（这一部分的具体方案数可以一开始 DP 一下，其实就是个组合数）可以发现合法的不同的值的个数是一个区间，差分最后算一下就行。

另外还要算一下不存在 $i$ 和 $i+1$ 同时存在的情况就行。

9.28

ACL Contest 1

A - Reachable Towns

先按 $x$ 坐标排序，$y$ 坐标的顺序对连边求连通块大小。

显然一个连通块肯定是一个区间。

前缀 $\min$ 和后缀 $\max$ 求出分界点就行。

B - Sum is Multiple

显然问题等价于求一个最小的正整数 $k$ 满足 $k(k+1) \bmod n=0$。

$k$ 和 $k+1$ 互质，于是对于 $n$ 的一个质因数肯定属于两者之一。

枚举 $n$ 的因数 $i$，且满足 $(i,\dfrac{n}{i})=1$，问题转化为求一个不定方程（$x\cdot i+y \cdot \dfrac{n}{i}=1$）的解。

C - Moving Pieces

看数据范围感觉就是个网络流。

原点往每个硬币连流量为 $1$，费用为 $0$ 的边。

每个不是障碍的点往下面和右边不是障碍的点连流量为无穷，费用为 $-1$ 的边。

每个不是障碍的点往汇点连流量为 $1$，费用为 $0$ 的点。

跑费用流即可。

D - Keep Distances

每个点往它后面第一个距离它至少为 $k$ 和它前面第一个距离它至少为 $k$ 的点连边。

显然对于一个询问 $[l,r]$ 在答案集合内的点是下图中画横线中间的点。

可以倍增算出所有合法区间的右端点之和和所有合法区间的左端点之和。

然后就做完了。

E - Shuffle Window

问题显然可以转化为每次把 shuffle 的一个数加入序列的末尾，然后在 shuffle 的数中加入一个数。

考虑对每一对满足 $i<j$ 的权值 $(i,j)$ 算贡献。

懒得具体写式子了，直接放个暴力的代码吧。

For(i,2,n) FOR(j,1,i){
	int x=p[i],y=p[j],ret=0,nw=1;
	FOR(l,max(1,x-k+1),max(1,y-k+1)){
		ret=(ret+nw)%mod;
		nw=1ll*nw*inv[k]%mod*(k-1)%mod;
	}
	ans=(ans+1ll*ret*inv[k])%mod;
}
For(i,1,n) For(j,i+1,n){
	int x=i,y=j,ret=0,nw=0;
	nw=power(1ll*inv[k]*(k-1)%mod,max(1,y-k+1)-max(1,x-k+1));
	FOR(l,max(1,y-k+1),n){
		ret=(ret+1ll*nw*inv[min(k,n-l+1)])%mod;
		nw=1ll*nw*inv[min(k,n-l+1)]%mod*(min(k,n-l+1)-2)%mod;
	}
	ans=(ans+ret)%mod;
}

其中 $inv[k]$ 表示 $k^{-1}$，$p[i]$ 表示权值 $i$ 的下标。

大概是分类讨论 $p_i$ 和 $p_j$ 大小关系，在 $i$ 加入后 $j$ 加入之前，每次必须不能选到 $i$，之后枚举什么时候会删除 $i$，删除之前不能选两者之一。把这个代码写出来后会发现两部分好像是独立的，于是就有了上面的代码。

上面的代码就很好优化了，第一段可以从小到大加入每个数，线段树随便维护一下。

第二段随便化化式子就可以做到 $O(n)$ 的。

F - Center Rearranging

首先 $B$ 中肯定有连续一段是 $A$ 没动的数组成的，将它们称为 M 类型数； M 左边是由于 push_front 操作而得到的称为 L 类型数； M 右边是由于 push_back 操作而得到的称为 R 类型数。

最终 $B$ 肯定是长 L...LM...MR...R 这样的，我们可以枚举 M 的区间，这样 $B$ 所有数是怎么得到的就确定了。

考虑对每三个 $x$，$B$ 中每个 $x$ 对应了 $A$ 中的哪个 $x$。

先考虑 $B$ 中这三个数(位置从小到大)都分别是怎么操作得到的，共有 10 中可能，其中 LLL 和 RRR 显然肯定是不可能。

剩下的八种情况就需要自己手玩了，具体可以见下表。

A:M** ***
B:LMR LLR 我们称这两组是第一种类型

A:**M ***
B:LMR LRR 我们称这两组是第二种类型

A:M** **M MMM M*M M*M
B:MRR LLM MMM LMM MMR 我们称这五组是第三种类型

可以发现除了 LMR 之外，所有 M 的在 $A$ 中的位置其实是确定的。

确定 M 的位置可以来帮助我们确认当前划分方案是否有解，对于所有 M，如果其在 $A$ 的位置和其在 $B$ 的位置连一条边，显然这些边如果相交了就无解了，因为 M 是不会动的，所有原先在左边的不可能跑到右边去。

我们先来考虑如果有解最小步数是多少，不难发现，其实就是 $3n-cntM$，$cntM$ 表示 $M$ 的个数，这显然是答案的下界，也显然能构造一种合法的操作方案。

现在先考虑如果每个 LMR 是什么类型都确定了，怎么判是否有解。

首先可以发现，第一、二组不同于第三组的地方是，第一、二组的 L 和 R 的操作顺序会多一些限制，比如第一组中 LLR，第一步必须是 push_back。

考虑这样一个图 $G$，图中一条边 $u \to v$ 表示，$u$ 必须必 $v$ 先操作。所以对于第一种类型，第三个在 $B$ 中的位置向第一个在 $B$ 中的位置连一条边；对于第二组同理。另外还有就是右边的 L 向左边的 L 连边，左边的 R 向右边的 R 连边。如果图 $G$ 不存在环，就可以按照拓扑序做操作；否则，这说明无解。

可以发现这个图非常特殊，如果存在环，只能是一个某个第一种类型的第一、三位置都比某一个第二种类型更小。

于是现在问题转化为是否存在一种确定每个 LMR 属于第一个类型还是第二个类型的方案，使得上面的条件都满足。

不难发现所有限制都是一个二元限制，每个 LMR 有两种选择，所以我们可以用 2-sat 判是否有解。

10.2

AGC 034

A - Kenken Race

如果 $C<D$，$B$ 先跳到 $D$，$A$ 再跳，只要判下 $[A,D]$ 是否存在两个连续的障碍就行。

否则，$[B,D]$ 还需要存在一个长度至少为 $3$ 的空地，让 $B$ 跳到中间，让 $A$ 跳过 $B$。

B - ABC

随便数吧。

C - Tests

注意到最终不是满分或者零分的科目最多只有一个。

二分答案后，枚举不是满分或者零分的科目，满分的科目肯定取 $b_i\times l_i+(X-b_i)\times r_i$ 最大的那几个。

D - Manhattan Max Matching

众所周知绝对值里面的正负号如果取错，答案肯定比取对小。

于是把每个点拆成四个点，分别表示每个坐标前取什么符号的四种情况，红球和蓝球对应的再往一个中间点连边就行。

感觉可以模拟费用流，但是不太会这个东西，先鸽着。

E - Complete Compress

先枚举最终所有点聚到哪个点。

注意到一个子树可行的还需要的操作次数是一个区间，这里的操作是指操作的两个点一个点在这个子树内，一个点在这个子树外。

于是随便 dp 下就行。

F - RNG and XOR

~~AGC 抄袭 ZJOI 石锤~~

令 $f_S$ 表示 $S$ 的答案，为表示方便 $p_i = \frac{p_i}{\sum_{i}p_i}$。

对于 $S\ne \varnothing$，有：

\[f_S=1+\sum_{T} p_T f_{S\oplus T}\]

令 $G=\sum_{S} p_Sx^S$，$F=\sum_{s} f_sx^s$ 为集合幂级数。

于是可以得到：

\[F=\sum_{S}x^S+F\times G+cx^{\varnothing}\]

因为 $f_0=0$ 所以 $c$ 为一个需要确定的待定系数。

考虑先对该式做 FWT。

令 $\widetilde{F}$ 为 $F$ 的 FWT 结果，可以得到：

\[[x^S]\widetilde{F}\times(1-[x^S]\widetilde{G})=\sum_{T} (-1)^{|T\cap S|} +c\]

当 $S=\varnothing$ 时，$[x^{\varnothing}]\widetilde{G}=1$，所以左式为 $0$，所以可以得到 $c=-2^n$。

对于其他 $S\ne\varnothing$ ，$[x^{S}]\widetilde{G}<1$，所以可以得到 $[x^S]\widetilde{F}=\dfrac{c}{1-[x^S]\widetilde{G}}$。

做 IFWT，得到：

\[f_S=\dfrac{1}{2^n}\sum_{T}(-1)^{|S\cap T|} [x^T] \widetilde{F}=\dfrac{[x^{\varnothing}] \widetilde{F}}{2^n}-\sum_{T\ne \varnothing} (-1)^{|S\cap T|} \dfrac{1}{1-[x^T]\widetilde{G}}\]

因为 $f_{\varnothing}=0$，可以得到：

\[\dfrac{[x^{\varnothing}] \widetilde{F}}{2^n}=\sum_{T\ne \varnothing} (-1)^{|S\cap T|} \dfrac{1}{1-[x^T]\widetilde{G}}\]

所以最终可以得到：

\[f_S=\sum_{T\ne \varnothing} (1-(-1)^{|S\cap T|}) \frac{1}{1-[x^T]\widetilde{G}}\]

以上内容基本抄自 lyx 「ZJOI2019」开关的题解。

令 $g_i=\dfrac{1}{1-[x^T]\widetilde{G}},h_i=[\text{popcount}(i) \bmod 2=1]$。

则原式为：

\[f_S=\sum_{T} g_Th_{S\cap T}\]

注意到这是一个 $\text{BITANDMUL}(g)$ 的转置。

对 $h$ 做的变换都是转置的就行。

10.4

ARC 104

D - Multiset Mean

直接背包就完事了。

E - Random LIS

暴搜大小关系，然后就是划艇了。

F - Visibility Sequence

可以发现一个 $P$ 序列对应一棵笛卡尔树。

于是转为 dp 笛卡尔树的结构。

令 $f_{l,r,i}$ 表示区间 $[l,r]$ 根的值为 $i$ 有多少种不同的笛卡尔树结构。

为了防止算重每个点的值尽量要小，根据这个转移就行，也就是当前根的值为 $\max(val_{lson},val_{rson}+1)$。

可以前缀和优化到 $O(n^4)$，但是显然不优化 $O(n^5)$ 也能过。

10.10

写题解好麻烦啊，好几场一起写了吧。

AGC 033

A - Darker and Darker

等价于求所有 . 到某个 # 最短路的最大值。

B - LRUD Game

注意到每个方向是独立的。

C - Removing Coins

注意到和只有一条直径是等价的。

D - Complexity

直接 DP 是 $O(n^5)$ 的时间和 $O(n^4)$ 的空间的。

注意到答案是 $O(\log n)$ 级别的，并且如果固定左、上、下边界，随着右边界的增大，答案递增。

于是把 DP 的一维换成答案，转为 DP 右边界就行。

考虑先枚举答案就能转移了。

双指针一下可以做到 $O(n^3\log n)$，不过 $O(n^3\log^2 n)$ 也能过。

E - Go around a Circle

假设第一个字母是 R，可以发现最终序列需要满足以下两个性质：

不能有相邻的 B。
每段连续的 R 长度是奇数的，并且长度的限制是不小于 $S$ 第一段的长度最小的奇数和 $S$ 另外所有长度为奇数的段的长度的 $\min$。

具体证明并不难。

于是随便算算就行。

F - Adding Edges

可以看 nealchen的题解。

AGC 032

A - Limited Insertion

从前往后一个一个插入就行。

B - Balanced Neighbors

完全图去掉 $i$ 和 $n-(n \bmod 2)-i$ 的边就行。

C - Three Circuits

首先显然要每个点度数都是偶数。

如果边数大于 $n+2$ 肯定有解，小于 $n+2$ 肯定无解。

边数等于 $n+2$ 的时候，有一种情况会无解，大概是类似于一个西瓜的形状，两个度为 $4$ 的中间连了四条链，另外都是有解的。

D - Rotation Sort

显然如果操作了肯定是一步到位，于是一次操作可以认为是插入一个数。

DP 的时候记最后一个没动的数就行。

可以做到 $O(n\log n)$，具体可以看 wzp 9102 年的集训队作业。

E - Modulo Pairing

我们先最终配对的两个点 $x+y$ 的值大于 $m-1$，则把这两个数称为第一类数，否则则称为第二类数。

如果每个点确定了种类，则每个种类肯定是最小和最大配，第二小和第二大配...这样配。

又可以发现最终答案的配对方案肯定存在一种是，前 $k$ 大的数是第一类数，另外的数是第二类数，具体可以通过调整法证明。

于是我们得到了一个 $O(n^2)$ 的做法。

考虑二分答案，可以发现可以作为第一类数的是一个后缀，可以作为第二类数的是一个前缀，如果有一个数既不能是第一类数也不能是第二类数则无解，另外还需要第二类数的配对满足条件。

F - One Third

~~感觉像是个知乎题。也确实一部分结论在知乎看到过。~~

可以看这里。

ExaWizards 2019

C - Snuke the Wizard

注意到最后不会出去的是一个区间，二分一下左右边界就行。

D - Modulo Operations

如果在 $\bmod x$ 之前先 $\bmod$ 了一个小于等于 $x$ 的数 $y$，则 $\bmod x$ 是无效的。

于是从大到小插入一个 $a_i$ 随便 DP 下就行。

大概转移就是考虑当前数是否有效，无效就是插到了后面的 $n-i$ 个位置中的一个。

E - Black or White

枚举下最后一段长度然后随便算算。

F - More Realistic Manhattan Distance

把有用的几条路抠出来跑最短路就行。

有用的大概是起点和终点上下左右某个方向的第一条路。

10.15

写题解好麻烦啊，以后只记想记的题吧。

AGC 031

C - Differ by 1 Bit

可以发现如果 $A,B$ 差奇数位才有解。

考虑怎么构造区间 $[l,r]$ 的答案，把 $a_{mid}$ 和 $a_{mid+1}$ 设置成只有一位不同且和 $a_l$ 和 $a_r$ 有奇数位不同，设 $a_{mid}$ 和 $a_{mid+1}$ 不同的那一位是第 $k$ 位，则还需要把 $[l,mid-1]$ 第 $k$ 位设置和 $a_{mid}$ 相同，把 $[mid+1,r]$ 第 $k$ 位设置和 $a_{mid+1}$ 相同，递归构造 $[l,mid]$ 和 $[mid+1,r]$ 就行。

正确性可以归纳。

D - A Sequence of Permutations

可以发现运算 $f(p,q)=q\cdot p^{-1}$。

手动算出 $f$ 的前几项，可以发现有规律。

E - Snuke the Phantom Thief

枚举选了几个，每个 $x$ 的前缀选了几个必须在一个区间内，$y$ 同理。

考虑根据这个建图，一共两排点，一排表示 $x$ 的前缀和一排表示 $y$ 的前缀。

$x$ 和 $y$ 对应的连一条流量为 $1$ 费用为对应价值的边，两排点建流量有上下界，费用为 $0$ 的边表示区间的限制就行。

注意到最大流肯定是费用最大的，于是跑上下界最大费用可行流就行。

F - Walk on Graph

考虑倒着考虑这个过程。

令 $(u,x)$ 表示当前在 $u$，值为 $x$，如果存在一条 $(u,v,c)$ 的边，则可以从 $(u,x)$ 到 $(v,2x+c)$，注意到模数是一个奇数，$2$ 存在逆元，所以 $x$ 和 $2x+c$ 是一一对应的，$2x+c$ 一直走一定能走回 $x$，所以 $(u,x)$ 和 $(v,2x+c)$ 能互相到达。

然后如果一个点存在边权为 $a$ 和 $b$ 的连边，那么如果我们这样走：

\[(v,4x+3a) \rightarrow (u,x) \rightarrow (v',4x+3b)\]

可以得到 $(u,x)$ 能到达 $(u,x+3k(b-a))$，因为 $4$ 存在逆元，所以 $4x$ 可以是 $[0,mod)$ 中任意一个数。

考虑到整个图是连通的，令 $g$ 表示两两边权的在模域下的差的 $\gcd$，模数可以改成 $\gcd(3g,mod)$，由于 $g|(a-b)$ 且 $g|(b-a)$ 所以 $g$ 肯定整除 $mod$，所以新模数肯定是 $g$ 或者 $3g$。

所有 $C_i$ 在模 $g$ 域下是同余的，这样每个边权 $C_i$ 可以表示成 $c_ig+b$ 的形式，我们还可以通过一些处理，去掉 $b$。

我们把所有的当前的值 $x$ 都加上 $b$，所有边权都减去 $b$，可以发现这样转化后问题和原问题是等价的。

\[x'-b=x\rightarrow (2x+c_ig+b)=(2(x+b)+c_ig)-b=(2x'+c_ig)-b\]

于是我们可以把所有边权减去 $b$，每次询问改成 $(t,b)$ 能否达到 $(s,b+r)$。

注意到从 $(u,x)$ 出发能到达的状态一定能表示成 $(v,2^px+qg)$ 的形式，显然 $q$ 的取值只能是 $\{0,1,2\}$。

另外注意到 $(u,x) \rightarrow (u,4x+3c_ig)=(u,4x)$，所以所有 $2^px+qg$ 中 $p$ 的奇偶性相同的点又可以缩起来，那一共就只剩下 $O(6n)$ 个点了。

查询就是询问是否存在一对 $p,q$ 满足 $r+b=2^pb+qg$，预处理 $2^{p}b$ 的点有哪些就可以快速判断了。

复杂度 $O(m\log mod+6(m+q)\alpha(n)+mod)$。

ARC 105

F - Lights Out on Connected Graph

问题等价于求生成连通二分图计数。

首先有一个显然不对的计算方法。

枚举每个点处于这个二分图左边还是右边，每条连接左边和右边的点的边有选不选都可以，只连接左边和左边的边不能选，右边同理。

可以发现这样算每个生成二分图会被计算 $2^k$ 次，$k$ 表示连通块数。

令 $f_S$ 表示集合 $S$ 中的点生成连通二分图的个数，$g_S$ 表示集合 $S$ 中的点生成二分图的个数，$h_S$ 表示集合 $S$ 中的点用上面的计算方法得到的答案。

可以发现对于一个有 $k$ 个连通块的生成二分图，把这个图分成两部分使得每一部分都是二分图的方案也是 $2^k$。

于是我们可以得到 $g^2=h$。

又可以通过 $f=\ln g$ 得到 $f$ 而得到答案。

Yahoo Programming Contest 2019

没啥好记的。

10.19

NIKKEI Programming Contest 2019

E - Weights on Vertices and Edges

按边权从小到大加边，每次加边的时候如果不合法就先加进去，如果后面这个连通块加边成功了就算上之前加入但不合法的边。

F - Jewels

把每个颜色最大的两个捆绑，每种颜色要先加入捆绑的才能加入单个的。

每次加入一个新的有四种方案：

直接加入一个单个的。
删除一个单个，加入一个捆绑的。
删除一个捆绑的，加入一个颜色的捆绑的和一个单个的。
删除一个单个和一个捆绑的，加入两个捆绑的。

于是五个堆维护一下就行。

KEYENCE Programming Contest 2019

没啥好记的。

10.21

AGC 030

会做 A,B,D,F，这几题也没啥高论，就记下我不会的题吧。

C - Coloring Torus

构造苦手。

如果 $K\le 500$，一行放一种数就行；

如果 $K>500$，可以在同一对角线上交替放两种颜色。

E - Less than 3

思维题苦手。

在一个串的每个 $01$ 子串中放一个红色的标记，每个 $10$ 子串中放一个蓝色标记。

发现修改就是把某个标记移动一格，或者在头尾加入/删除一个标记，并且需要满足任意两个相邻标记之间的距离小于等于 $2$。

考虑枚举两个串标记的匹配关系，对于一组对应关系，下界显然是对应的线之间的距离之和，并且这个下界是可以构造达到的。

10.24

ARC 106

E - Medals

考虑二分答案。

考虑这样一个二分图，左边部分第 $i$ 个点表示第 $i$ 天，右边部分 $n\times k$ 个点分别表示每个点的需求，左边第 $i$ 个点往右边能发奖牌的点连边，判断是否合法即判断该图是否存在一个完美匹配。

考虑 Hall 定理，对于右边的每个人的集合 $S$，求左边有多少天至少和 $S$ 中的一个点匹配的，记为 $F_S$。

令 $G_S$ 表示左边有多少天和 $S$ 中每一个点都能匹配，可以发现 $F_S=\sum_{T\in S} (-1)^{|T|+1}G_{T}$。

又可以发现答案是 $O(nk)$，于是我们可以预处理出第 $i$ 天能和哪些人配，记为 $b_i$，令 $cnt_S=\sum_{i}[b_i=S]$，可以发现对 $cnt$ 做一遍高维后缀和就能得到 $G$，再对 $G$ 做高维前缀和就能得到 $F$ 了。

时间复杂度 $O(2^nn\log nk+nk\log nk+n^2k)$。

F - Figures

考虑 prufer 序列。

答案的式子为 $(n-2)!\sum_{\sum_{i}cnt_i=n-2} \prod_{i} \frac{d_i!}{cnt_i!(d_i-cnt_i-1)!}$。

把后面的形式改改 $(n-2)!\sum_{\sum_{i}cnt_i=n-2} \prod_{i} d_i \binom{d_i-1}{cnt_i}$。

把 $d_i$ 提出来，可以发现后面是个范德蒙德卷积，也可以考虑组合意义，不难发现就是 $\binom{\sum_{i} d_i-1}{n-2}$。

10.29

AGC 029

A,B,C,D,E 感觉都挺 easy 的，就不记了。

F - Construction of a tree

~~一开始就走偏了，如果想到怎么判无解应该就会往二分图方向想，应该就会了吧~~

定义一个 $\{1,2,..,N\}$ 的非空子集的 $S$ 邻集 $N(S)$ 是所有在其中出现 $S$ 的点的集合。

大力猜一波，如果对于任意 $S$ 都满足 $|N(S)|\ge |S|+1$ 就肯定存在解。

这个条件的必要性显然，并且如果满足这个条件，根据 Hall 定理，这个二分图肯定存在一个完美匹配。匹配后会剩下一个点没有匹配，不妨设它为根，我们考虑搞出一个顺序，按顺序让每个集合匹配的点找到一个父亲，满足在这个顺序下父亲在它之前被考虑，这个直接从根开始 bfs 就行。

然后我们可以发现如果满足了上面这个条件，这样构造就必然存在解。

如果 bfs 在中途就结束了，那么走过的左边点个数比右边点个数多 $1$，左边点总个数比右边点总个数多 $1$，故现在未遍历的右边的点的集合 $T$ 满足 $|N(T)|\le |T|$，这与命题矛盾。

如果用 Dinic 跑二分图匹配，复杂度是 $O(m\sqrt{n})$ 的，但是这个题直接跑匈牙利就能过。

AGC 028 很早就补完了，独立做了 A,B,C,D,E 和 F 的大常数 $O(n^3)$ 但是觉得有些东西我不知道怎么用文字描述所以题解就先鸽着。

另外因为联赛训练的缘故，AGC 的补题就先搁置了。

9.2